Mukammal aylana chiziqdan hosil bo'ladi, unda har qanday nuqta o'z markazidan mukammal teng masofada joylashgan bo'lib, uning shaklida aniq dizaynga erishadi. Bunday tushunchani osongina tushunish mumkin va biz, ehtimol, har kuni bu dumaloq mukammallikka erishadigan dizayn yoki ob'ektlarga duch kelamiz. Biroq, real hayotda va g‘oyalar doirasidan tashqarida mukammal doira mavjud emas va unga erishib bo‘lmaydi, lekin buni sinab ko‘rish mumkin: bu amerikalik dasturchi Nil Agarvalning “Mukammal doira chizish” veb-saytida qo‘ygan muammosi.
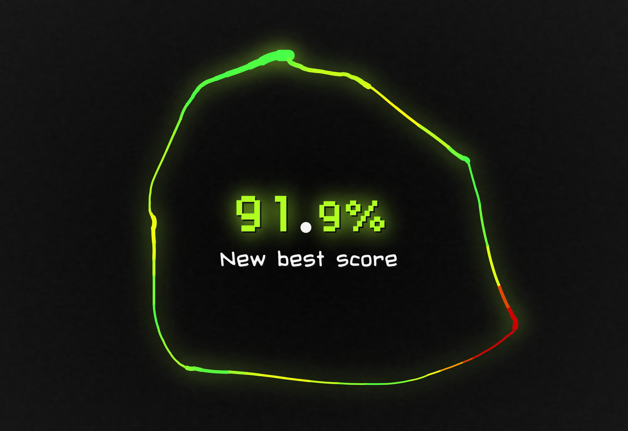
Chizma rang bo'yicha ham to'g'ri egri chiziqqa yaqinligi yoki xatoning intensivligini ko'rsatadi
-Nima uchun sayyoralar, oylar va yulduzlar doimo yumaloq bo'ladi? ?
Sayt unvoni ko'rsatganidek sodda va foydalanuvchini mukammal doira chizishga taklif qiladi. Uning soddaligiga mutanosib ravishda taklifnoma nihoyatda o'ziga qaram bo'ladi. Har bir urinishdan so'ng, foizlar ular ideal sohaga qanchalik yaqin yoki uzoq bo'lganliklarini tashxis qiladi - va hatto real hayotning 100% imkonsizligini bilsa ham, uni chizishga urinishdan to'xtab qolishning iloji yo'qdek tuyuladi. Sayt Mac va shaxsiy kompyuterlarda, shuningdek, smartfonlarda ishlaydi.
Shuningdek qarang: Munozarali hujjatli film gomofobik zo'ravonlikka qarshi kurashayotgan birinchi LGBT to'dasini tasvirlaydi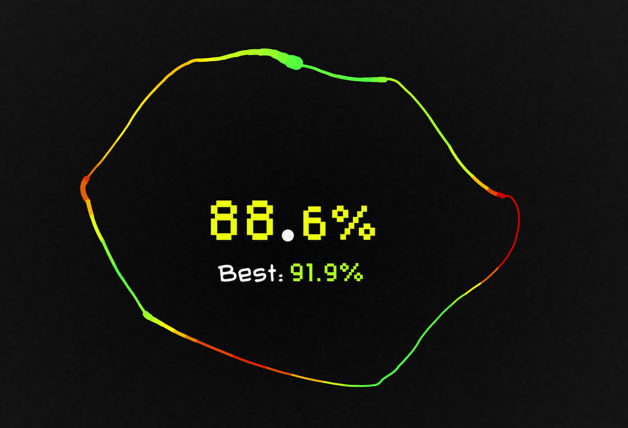
Foyizning aniqligi ham shubhali, ammo chizishga urinishdan to'xtab bo'lmaydi
-Yerning og'irligi hozir 6 ronnagram: yangi vazn o'lchovlario'rnatilgan
Oddiy raqamli chalg'itishdan tashqari, mukammal doira - va uning aniq imkonsizligi - inson tafakkuri uchun ajoyib mavzu bo'lib, unga hatto yunon faylasufi Platon ham duch kelgan va u tushunchani yagona deb ta'kidlagan. g'oyalar yoki shakllar nazariyasi misollari. Platonning so'zlariga ko'ra, biz mukammal aylana g'oyasini qanday qabul qilishni osonlikcha bilsak ham, u shunchaki mavjud emas, xuddi mukammal to'g'ri chiziq yo'qligi kabi. G'oyalar yoki matematika mavhumligidan tashqari, bu illyuziya bo'lar edi, chunki yaqindan uning nomukammalliklari va noaniqliklari doimo paydo bo'ladi.

Olim Arnold Nikolaus qo'lida kremniy shar bilan Germaniya.
- O'zingizni chalg'itishning imkonsiz shaffof jumboqlari va boshqa variantlari
Bir nechta ilmiy loyihalar ushbu dilemmani hal qilishga intildi. mumkin bo'lgan eng yumaloq ob'ekt. Koinotda ma'lum bo'lgan eng dumaloq samoviy jism - Kepler 11145123 yulduzi bo'lib, u Yerdan 5 ming yorug'lik yili uzoqlikda joylashgan bo'lib, radiusi 1,5 million kilometrni tashkil etadi: ekvator va qutb radiusi o'rtasidagi farq bor-yo'g'i 3 kilometr - baribir, farq, Bu ma'lum bo'lgan eng mukammal tabiiy ob'ektning nomukammalligini takrorlaydi. Shu bilan birga, siz smartfoningiz da eng ko'p o'ziga qaram qiladigan sayt orqali mukammallikni sinab ko'rishingiz mumkin.bugun.
Shuningdek qarang: Bu asalarichi o'z asalarilarini marixuana o'simligidan asal ishlab chiqarishga muvaffaq bo'ldi
Deyarli mukammal kremniy sferasi konventsiyada kilogramm o'lchovini qayta aniqlash uchun ishlatilgan
