ഏതു ബിന്ദുവും അതിന്റെ കേന്ദ്രത്തിൽ നിന്ന് തികച്ചും തുല്യമായ ഒരു രേഖയാൽ രൂപംകൊള്ളുന്നു, അതിന്റെ ആകൃതിയിൽ കൃത്യമായ രൂപരേഖ കൈവരിക്കുന്നു. അത്തരമൊരു ആശയം എളുപ്പത്തിൽ മനസ്സിലാക്കാവുന്നതേയുള്ളൂ, മാത്രമല്ല ഈ വൃത്താകൃതിയിലുള്ള പൂർണ്ണത കൈവരിക്കുന്നതായി തോന്നുന്ന ഡിസൈനുകളോ വസ്തുക്കളോ ഞങ്ങൾ മിക്കവാറും എല്ലാ ദിവസവും കണ്ടുമുട്ടുന്നു. പക്ഷേ, യഥാർത്ഥ ജീവിതത്തിലും ആശയങ്ങളുടെ മണ്ഡലത്തിന് പുറത്തും, തികഞ്ഞ വൃത്തം നിലവിലില്ല, അത് നേടാൻ കഴിയില്ല - എന്നാൽ ഇത് പരീക്ഷിക്കാം: അമേരിക്കൻ പ്രോഗ്രാമർ നീൽ അഗർവാൾ ഡ്രോ എ പെർഫെക്റ്റ് സർക്കിൾ എന്ന വെബ്‌സൈറ്റിൽ ഉയർത്തുന്ന വെല്ലുവിളി ഇതാണ്.

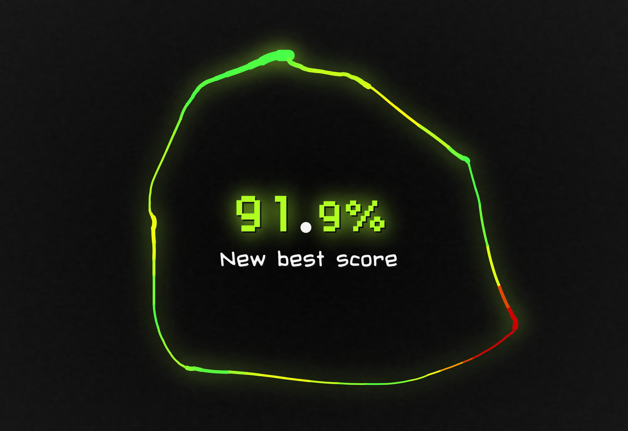
ചിത്രം, ശരിയായ വക്രത്തിന്റെ സാമീപ്യത്തെയോ പിശകിന്റെ തീവ്രതയെയോ നിറംകൊണ്ട് സൂചിപ്പിക്കുന്നു

-എന്തുകൊണ്ടാണ് ഗ്രഹങ്ങളും ഉപഗ്രഹങ്ങളും നക്ഷത്രങ്ങളും എല്ലായ്പ്പോഴും വൃത്താകൃതിയിലുള്ളത് ?

സൈറ്റ് അതിന്റെ ശീർഷകം സൂചിപ്പിക്കുന്നത് പോലെ ലളിതമാണ്, കൂടാതെ മികച്ച വൃത്തം വരയ്ക്കാൻ ശ്രമിക്കുന്നതിന് ഉപയോക്താവിനെ ക്ഷണിക്കുന്നു. അതിന്റെ ലാളിത്യത്തിന് ആനുപാതികമായി, ക്ഷണം അവിശ്വസനീയമാംവിധം ആസക്തി നിറഞ്ഞതാണ്. ഓരോ ശ്രമത്തിനും ശേഷം, ഒരു ശതമാനം അവർ ആദർശമണ്ഡലത്തിൽ നിന്ന് എത്ര അടുത്തോ അകലെയോ വന്നിരിക്കുന്നുവെന്ന് നിർണ്ണയിക്കുന്നു - കൂടാതെ യഥാർത്ഥ ജീവിതത്തിന്റെ 100% യഥാർത്ഥത്തിൽ അസാധ്യമാണെന്ന് അറിയാമെങ്കിലും, അത് വരയ്ക്കാനുള്ള ശ്രമം നിർത്തുന്നത് അസാധ്യമാണെന്ന് തോന്നുന്നു. സൈറ്റ് Mac, PC എന്നിവയ്‌ക്കും സ്‌മാർട്ട്‌ഫോണുകളിലും പ്രവർത്തിക്കുന്നു.

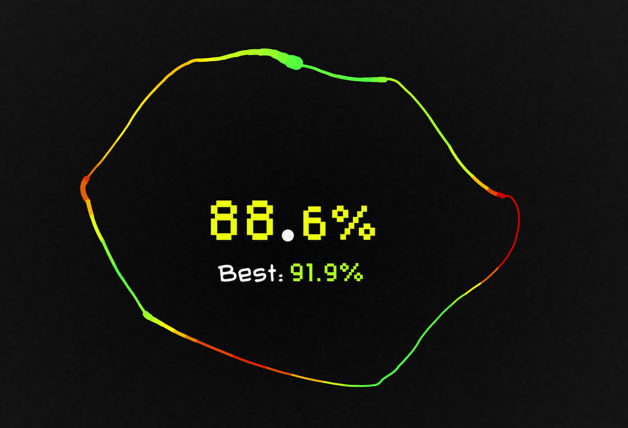
ശതമാനം കൃത്യതയും സംശയാസ്പദമാണ്, പക്ഷേ വരയ്ക്കാൻ ശ്രമിക്കുന്നത് നിർത്തുക അസാധ്യമാണ്

-ഭൂമിക്ക് ഇപ്പോൾ 6 റോണ്ണഗ്രാം ഭാരമുണ്ട്: പുതിയ ഭാര അളവുകൾസ്ഥാപിച്ചു

ലളിതമായ ഒരു ഡിജിറ്റൽ വഴിതിരിച്ചുവിടലിനുമപ്പുറം, തികഞ്ഞ വൃത്തം - അതിന്റെ മൂർത്തമായ അസാധ്യത - മനുഷ്യചിന്തയ്ക്ക് ഒരു മഹത്തായ വിഷയമാണ്, ഇത് ആശയത്തെ ഒന്നായി ചൂണ്ടിക്കാണിച്ച ഗ്രീക്ക് തത്ത്വചിന്തകൻ പ്ലേറ്റോ പോലും അഭിമുഖീകരിച്ചിരുന്നു. ആശയങ്ങളുടെ അല്ലെങ്കിൽ രൂപങ്ങളുടെ സിദ്ധാന്തത്തിന്റെ ഉദാഹരണങ്ങൾ. പ്ലേറ്റോയുടെ അഭിപ്രായത്തിൽ, ഒരു പൂർണ്ണ വൃത്തം എന്ന ആശയം എങ്ങനെ ആസ്വദിക്കാമെന്ന് നമുക്ക് എളുപ്പത്തിൽ അറിയാമെങ്കിലും, തികച്ചും നേർരേഖ ഇല്ലാത്തതുപോലെ അത് നിലവിലില്ല. ആശയങ്ങളുടെയോ ഗണിതത്തിന്റെയോ അമൂർത്തീകരണത്തിന് പുറത്ത്, അത് ഒരു മിഥ്യയാണ്, കാരണം, അടുത്ത്, അതിന്റെ അപൂർണതകളും കൃത്യതയില്ലായ്മകളും എല്ലായ്പ്പോഴും ദൃശ്യമാകും.

ജർമ്മനിയിൽ ഒരു സിലിക്കൺ ഗോളവുമായി ശാസ്ത്രജ്ഞൻ അർനോൾഡ് നിക്കോളാസ്

-സ്വയം വ്യതിചലിപ്പിക്കാനുള്ള അസാധ്യമായ സുതാര്യമായ പസിലുകളും മറ്റ് ഓപ്ഷനുകളും

ഒരു സിലിക്കൺ ബ്ലോക്കിൽ നിന്ന് ഈ പ്രതിസന്ധി പരിഹരിക്കാൻ നിരവധി ശാസ്ത്ര പദ്ധതികൾ ശ്രമിച്ചു. സാധ്യമായ ഏറ്റവും വൃത്താകൃതിയിലുള്ള വസ്തു. പ്രപഞ്ചത്തിൽ, അറിയപ്പെടുന്ന ഏറ്റവും വൃത്താകൃതിയിലുള്ള ആകാശഗോളമാണ് കെപ്ലർ 11145123, ഭൂമിയിൽ നിന്ന് ഏകദേശം 5 ആയിരം പ്രകാശവർഷം അകലെ, 1.5 ദശലക്ഷം കിലോമീറ്റർ ദൂരമുണ്ട്: മധ്യരേഖയും ധ്രുവ ദൂരവും തമ്മിലുള്ള വ്യത്യാസം 3 കിലോമീറ്റർ മാത്രമാണ് - ഇപ്പോഴും, ഒരു വ്യത്യാസം, അറിയപ്പെടുന്ന ഏറ്റവും മികച്ച പ്രകൃതിദത്ത വസ്തുവിന്റെ അപൂർണത ആവർത്തിക്കുന്നു. അതേസമയം, നിങ്ങൾ കണ്ടുമുട്ടുന്ന ഏറ്റവും ആസക്തിയുള്ള സൈറ്റിലൂടെ നിങ്ങളുടെ സ്‌മാർട്ട്‌ഫോണിൽ പൂർണ്ണത പരീക്ഷിക്കാംഇന്ന്.

കൺവെൻഷനിൽ കിലോയുടെ അളവ് പുനർ നിർവചിക്കാൻ ഏതാണ്ട് തികഞ്ഞ സിലിക്കൺ ഗോളം ഉപയോഗിച്ചു